The Basic Guide to Lambertian Reflectance
/The Basic Guide to Lambertian Reflectance
Venturing into the realm of optical intricacies, one encounters the phenomenon of Lambertian reflectance, a foundational concept that lies at the nexus of light interaction and material surfaces. Named after Johann Heinrich Lambert, this principle sheds light on the complex interplay between incident light and textured surfaces, offering profound insights into the behavior of light across various angles of observation. In this comprehensive examination, we delve into the profound world of Lambertian reflectance, exploring its theoretical origins, practical implications, and extensions.
johann lambert. not to be confused with christopher lambert. there can be only one.
Understanding Lambertian Reflectance
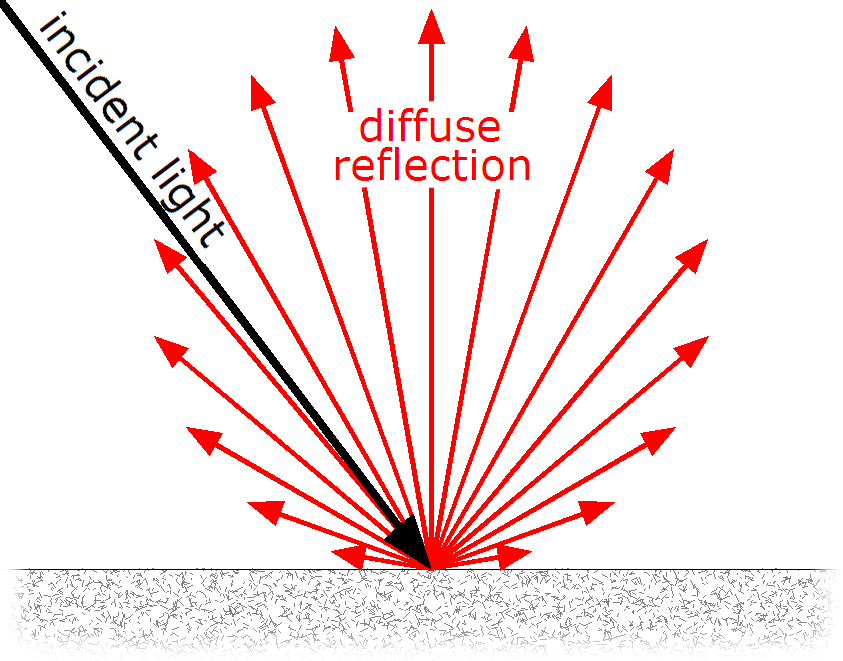
Lambertian reflectance forms the cornerstone of diffuse reflection theory, defining how light interacts with surfaces characterized by microscopic irregularities. It serves as a foundational model for the behavior of light across a diverse range of surfaces, encompassing everything from matte paintings to lunar landscapes. The essence of Lambertian reflectance lies in its uniformity of intensity across a wide field of view, irrespective of the observer's angle.
for lambertian distribution, uniformity of intensity is the name of the game
Theoretical Underpinnings: The Cosine Law and Uniform Intensity
Central to Lambertian reflectance is the cosine law, a geometric formulation dictating the intensity of light reflected from a surface. According to this principle, the intensity of light is directly proportional to the cosine of the angle between the incident light and the surface normal. This law underpins the even distribution of brightness across varying viewing angles, culminating in the uniform intensity characteristic of Lambertian surfaces.
A Complex Choreography of Light Diffusion
Lambertian reflectance's elegance emerges from the complex diffusion of light across a textured surface. As light interacts with microfacets of varying orientations, its trajectory becomes a dance of scattered paths. The aggregate effect of these scattered paths results in a uniform distribution of intensity, a phenomenon akin to observing a sea of stars from any vantage point.
To comprehend how the cosine law engenders Lambertian reflectance, envision a surface with microscopic facets oriented in various directions. As light impinges upon these facets, it adheres to the cosine law, dictating the intensity of each reflected ray. The aggregate effect of countless individual reflections, each governed by the cosine law, results in a distribution of scattered light that is both uniform and visually appealing.
Practical Implications and Applications
The practical utility of Lambertian reflectance extends across diverse fields:
Computer Graphics and Rendering: In the realm of computer graphics, Lambertian reflectance models serve as the bedrock for realistic rendering, ensuring accurate portrayal of light interactions within virtual scenes.
Computer Vision and Image Analysis: In the domain of computer vision, Lambertian surfaces facilitate illuminant-invariant feature extraction and robust object recognition.
Remote Sensing and Earth Observation: Lambertian reflectance proves indispensable in remote sensing applications, facilitating accurate data interpretation from satellite and aerial imagery, allowing for the detection of environmental changes and resource monitoring.
Challenges and Extensions
While Lambertian reflectance offers profound insights, its realm is not without complexities. Real-world surfaces often deviate from the idealized Lambertian model due to factors like anisotropic reflection, complex material properties, and the presence of specular highlights. Consequently, advanced models such as the bidirectional reflectance distribution function (BRDF) have emerged to address these challenges and provide a more comprehensive description of light-surface interactions.
Optical Diffusers and the Benefits of Lambertian Uniformity
Firebird optics diffusers- we like them so much we shot them into space
Optical diffusers are designed to scatter or spread light in a controlled manner, serving various purposes in optical systems, lighting, imaging, and displays. The choice of a Lambertian distribution for optical diffusers is rooted in its advantageous properties that make it particularly suited for certain applications. Here's why optical diffusers often strive to achieve a Lambertian distribution:
Uniform Illumination: Lambertian diffusers produce a uniform intensity distribution over a wide range of angles. This uniformity is crucial in applications where even lighting is essential, such as backlighting for displays or studio lighting in photography and videography.
Minimized Glare and Hotspots: Lambertian diffusion minimizes glare and the creation of bright spots or "hotspots." These undesirable effects can be problematic in applications where visual comfort is important, like architectural lighting or automotive displays.
Enhanced Viewing Angles: Lambertian diffusers offer a wider effective viewing angle for observers. This is beneficial for displays or signage that need to be viewed from various angles without significant loss of image quality or readability.
Homogenization: Lambertian diffusers help homogenize light by scattering it in multiple directions. This property is valuable in applications where a consistent level of brightness or color is desired, such as medical imaging or microscopy.
Reduced Specular Reflections: Specular reflections, which can cause unwanted glare, are minimized with Lambertian diffusers. This is valuable in situations where reflections need to be controlled, such as in automotive instrument clusters or outdoor displays.
Light Mixing: Lambertian diffusers efficiently mix light from different sources or colors, resulting in a more uniform color appearance. This is crucial in applications like LED lighting or projectors, where color consistency is paramount.
Optical Efficiency: Lambertian diffusers distribute light over a wide range of angles, making more efficient use of the emitted or incident light. This efficiency can be critical in energy-conscious applications.
Simplicity and Predictability: Lambertian scattering is well-understood and predictable, making it easier to design and model optical systems that incorporate diffusers with this behavior.
However, it's important to note that not all applications require Lambertian diffusion. In some cases, different diffusion patterns, such as Batwing or Gaussian distributions, might be more suitable to achieve specific lighting or optical effects. The choice of diffusion characteristics depends on the desired outcome and the specific requirements of the application.
Conclusion
Lambertian reflectance, a venerable concept steeped in the principles of optics, unveils the intricate dynamics between light and surfaces. From its theoretical origins to its applications in the realms of computer graphics, computer vision, and remote sensing, Lambertian reflectance offers an insightful lens through which we decipher the complexities of light diffusion. As we delve deeper into the nuanced interactions between light and matter, Lambertian reflectance remains an enduring cornerstone, guiding us through the intricate tapestry of optical behavior.
Here’s to your success!
Firebird Optics